반응형

LeetCode 문제 해석 및 풀이 방법
문제 74. Search a 2D Matrix(2D 행렬에서 찾기)
문제 설명
영문
You are given an m x n integer matrix matrix with the following two properties:
- Each row is sorted in non-decreasing order.
- The first integer of each row is greater than the last integer of the previous row.
- Given an integer target, return true if target is in matrix or false otherwise.
You must write a solution in O(log(m * n)) time complexity.
한글
두 개의 속성을 가진 m x n의 정수 행렬 matrix가 주어집니다.
- 각각의 행은 오름차순으로 정렬되어있습니다.
- 각 행의 첫번째 정수는 이전 행의 마지막 정수보다 큽니다
- 정수 target이 주어질 때, target이 있다면 True 아니면 False를 반환하십시오.
당신은 무조건 O(log(m * n))의 시간 복잡도를 가져야 합니다.
제한조건
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 100
- -10^4 <= matrix[i][j], target <= 10^4
입출력 예
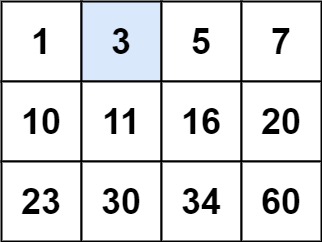
| 입력 | 출력 |
| matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3 | true |
| matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13 | false |
해답 및 해설
파이썬 (Python)
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
def search(nums: List[int], target: int, iscertain: bool=True) -> int:
left = 0
right = len(nums)-1
while left <= right:
mid = (right+left)//2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid -1
else:
return mid
if iscertain: return -1
if nums[mid] > target:
return mid-1
else: return mid
first_column = [l[0] for l in matrix]
row_idx = search(first_column, target, False)
if row_idx == -1: return False
column_idx = search(matrix[row_idx], target)
if column_idx == -1: return False
return True704. Binary Search의 코드를 재활용해서 행과 열에 대해 이진 탐색을 한 풀이. 열에 대해서 이진 탐색을 할 때에는 정확한 값이 아닌 그보다 작은 값의 idx를 찾도록 해주었고, 행에 대해서 이진 탐색을 할 때는 정확한 값을 찾도록 해줬다.
하지만 이 풀이는 열을 리스트로 뽑을 때 반복문을 쓰므로 시간 복잡도가 O(m*log n)이 될 수도 있겠다는 생각이 들었다. 이 사태를 피하려면 인덱스를 이용하는게 더 나을듯 싶다.
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
def search(iscolumn: bool=True, row_num:int=0) -> int:
left = 0
if iscolumn: right = len(matrix)-1
else: right = len(matrix[0])-1
while left <= right:
mid = (right+left)//2
if iscolumn: select = matrix[mid][0]
else: select = matrix[row_num][mid]
if select < target:
left = mid + 1
elif select > target:
right = mid -1
else:
return mid
if iscolumn:
if nums[mid] > target:
return mid-1
else: return mid
else:
return -1
row_idx = search(iscolumn=True)
if row_idx == -1: return False
column_idx = search(iscolumn=False, row_num=row_idx)
if column_idx == -1: return False
return True그래서 쓴 코드. 행일 때와 열일 때를 한 함수에 넣느라 복잡해지긴 했는데, 방식은 행과 열에서 각기 이진 탐색을 한다는 것은 똑같다.
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
m, n = len(matrix), len(matrix[0])
left, right = 0, m*n-1
while left<=right:
mid = (left+right)//2
if matrix[mid//n][mid%n]==target:
return True
if matrix[mid//n][mid%n]<target:
left = mid+1
else:
right = mid-1
return False찾아보니 2D 행렬을 하나의 단일한 배열로 생각한 후 이진 탐색을 하는 풀이도 있었다. 이렇게 해도 시간 복잡도가 똑같이 O(log(m * n))를 만족할 듯 싶다.
반응형
'🖥️ 문제 풀이 > 리트코드(Leetcode)' 카테고리의 다른 글
| [LeetCode 해석 및 풀이] 153. Find Minimum in Rotated Sorted Array (0) | 2024.04.22 |
|---|---|
| [LeetCode 해석 및 풀이] 875. Koko Eating Bananas (0) | 2024.04.21 |
| [LeetCode 해석 및 풀이] 704. Binary Search (0) | 2024.04.21 |
| [LeetCode 해석 및 풀이] 2. Add Two Numbers (0) | 2024.04.20 |
| [LeetCode 해석 및 풀이] 138. Copy List with Random Pointer (0) | 2024.04.20 |




댓글