반응형

순열과 중복순열 알고리즘을 파이썬으로 구현하기
순열이란?
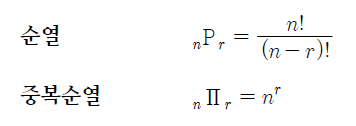
- 원소들을 순서에 따라 나열하는 것
- n개의 원소에서 r개를 나열한다 하면 그 가짓수는 n!/(n-r)!
- 중복해서 원소를 뽑으면 n^r
- 전체 순열 가짓수의 합은 조금 복잡하다. (링크)
여러가지 순열 알고리즘 구현해보기
기본 순열
n개의 원소를 가진 배열 arr에서 r개를 뽑아 나열한다.
swap을 이용한 방식
def permutations (arr, r):
n = len(arr)
results = []
def _perm_swap (arr, depth):
if (depth == r):
results.append(arr[:r])
return
for i in range(depth, n):
# 위치를 바꿈
arr[i], arr[depth] = arr[depth], arr[i]
_perm_swap(arr, depth+1)
# 다시 되돌림
arr[i], arr[depth] = arr[depth], arr[i]
_perm_swap (arr, 0)
return results
print(permutations([1,2,3], 2))
# [[1, 2], [1, 3], [2, 1], [2, 3], [3, 2], [3, 1]]
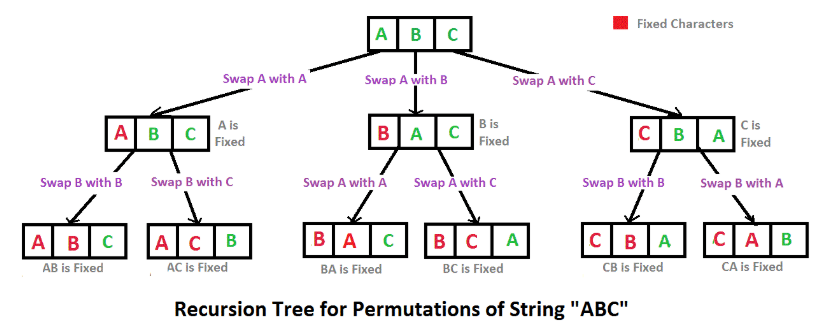
- 과정 : 0번째 인덱스 원소를 n-1번째까지 바꿔 고정한다. 그렇게 해서 나온 결과들을 다시 1번째, 2번째 인덱스에서도 하여 r번째 인덱스까지 반복한다. 인덱스가 r번째가 되면 앞의 r개만큼의 원소를 빼낸다.
- 특징 : 수열의 순서가 보장되지 않는다. 원래 배열을 건드림.
visited 배열을 이용한 방식
def permutations(arr, r):
n = len(arr)
visited = [False] * n
output = []
results = []
def _perm_visited(arr, visited, output, depth):
if (depth == r):
results.append(output[:])
return
for i in range(n):
if (visited[i]): #사용된 원소일경우 넘어감
continue
visited[i] = True
new_output = output + [arr[i]]
_perm_visited(arr, visited, new_output, depth + 1)
visited[i] = False
_perm_visited(arr, visited, output, 0)
return results
print(permutations([1, 2, 3], 2))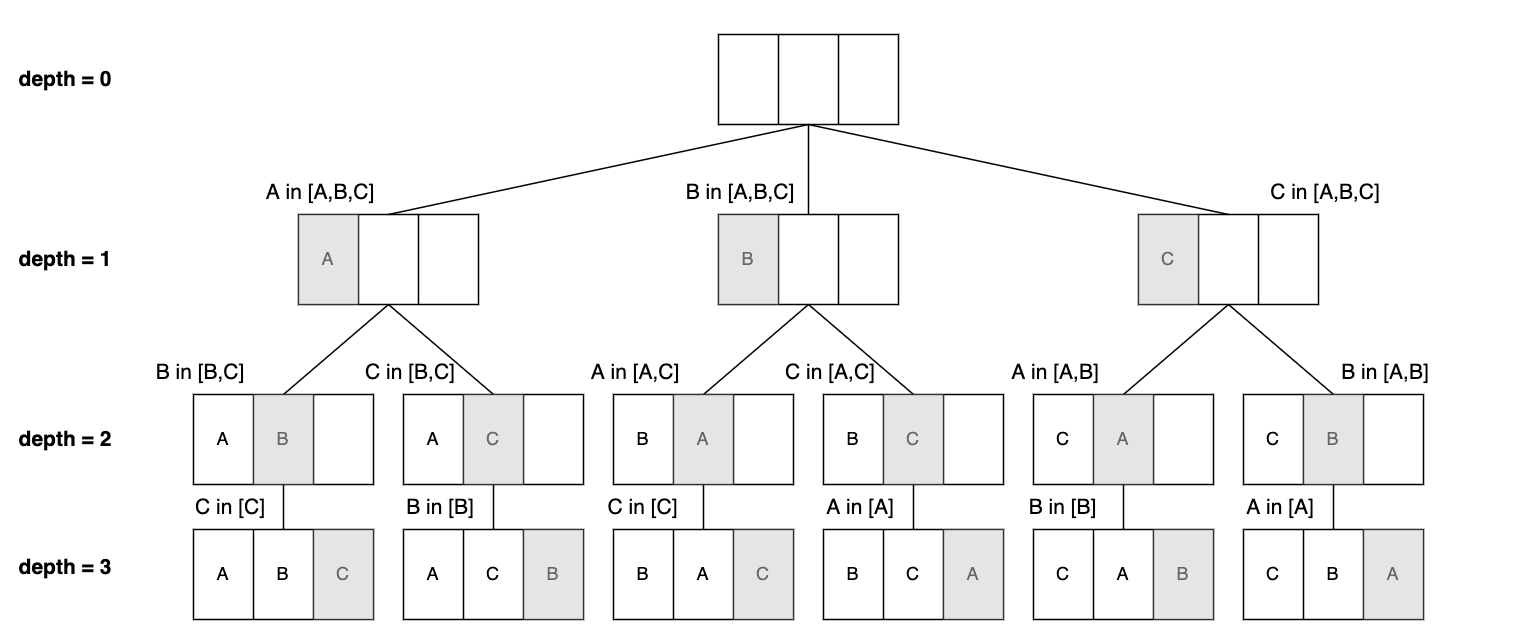
- 과정 : DFS를 돌며 모든 인덱스에 방문해 output에 넣음. 한번 넣은 원소의 인덱스는 visited 배열에 True로 표시해 중복을 막는다. 이 과정을 depth가 r이 될 때까지 반복한다.
- 특징 : 수열의 순서가 보장됨. 원 배열도 그대로 보장되지만 저장공간을 더 많이 사용하는 듯하다.
길이를 하나씩 늘려 재귀하는 방식
def permutation(arr, r):
result = []
if r == 0:
return [[]]
for i in range(len(arr)):
item = arr[i]
for rest in permutation(arr[:i] + arr[i+1:], r - 1):
result.append([item] + rest)
return result
print(permutation([1,2,3], 2))
Heap's algorithm을 이용한 순열
# 재귀 이용
def permutation(arr):
size = len(arr)
result = []
def _perm_heap(arr, size):
if size == 1:
result.append(arr[:])
return
for i in range(size):
_perm_heap(arr, size - 1)
if size & 1: # 홀수일 때
arr[0], arr[size - 1] = arr[size - 1], arr[0] #0번째를 맨 끝과 교체
else: # 짝수일 때
arr[i], arr[size - 1] = arr[size - 1], arr[i] #i번째를 맨 끝과 교체
_perm_heap(arr, size)
return result
a = [1, 2, 3]
print(permutation(a))
# 재귀 없는 버전
def permutation(arr):
size = len(arr)
result = []
result.append(arr[:])
count = [0] * size
i = 1
while i <= size - 1:
if count[i] < i:
if i % 2 == 0: k = 0
else: k = count[i]
arr[i], arr[k] = arr[k], arr[i]
count[i] += 1
i = 1
result.append(arr[:])
else:
count[i] = 0
i += 1
return result
a = [1, 2, 3, 4]
print(permutation(a))- 과정 : 홀짝에 따라 같은 교체를 반복하면 모든 순열 배열을 표시한다는 원리. 나중에 자세히 공부하자
- 특징 : 원소를 모두 배열하는 경우에만 사용 가능, 최소로 swap을 함
기타 알아볼 것
- Steinhaus–Johnson–Trotter algorithm
완전탐색 순열
순서있이 나열할 수 있는 모든 가짓수를 출력하기.
위의 순열을 모두 합치기
def permutation_all(arr):
n = len(arr)
result = []
for i in range(1, n + 1):
result += permutations(arr, i)
return result
print(permutation_all([1, 2, 3))
# [[1], [2], [3],
# [1, 2], [1, 3], [2, 1], [2, 3], [3, 2], [3, 1],
# [1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 2, 1], [3, 1, 2]]위에서 r개의 원소를 뽑아 순열을 구할 때 썼던 함수를 재이용해서 반복문을 돌려준다.
고정값을 하나씩 추가하는 방식
def permutation_all(arr):
result = []
def _perm_add(arr, fixed):
if len(arr) == 0:
return
for i in range(len(arr)):
new_fixed = fixed + [arr[i]]
result.append(new_fixed[:])
new_arr = arr[:i] + arr[i+1:]
_perm_add(new_arr, new_fixed)
_perm_add(arr, [])
return result
print(permutation_all([1, 2, 3]))
# [[1], [1, 2], [1, 2, 3], [1, 3], [1, 3, 2],
# [2], [2, 1], [2, 1, 3], [2, 3], [2, 3, 1],
# [3], [3, 1], [3, 1, 2], [3, 2], [3, 2, 1]]고정값을 하나 정해두고 거기에 다른 값을 덧붙이는 방식.
원소를 하나씩 추가하는 방식
def permutation_all(arr):
if len(arr) == 0:
return [[]]
new_item = arr.pop()
prev_perm = permutation_all(arr)
new_perm = []
for perm_item in prev_perm:
for idx in range(len(perm_item)+1):
new_perm.append(perm_item[:idx] + [new_item] + perm_item[idx:])
return prev_perm + new_perm
print(permutation_all([1, 2, 3]))
# [[],
# [1],
# [2], [2, 1], [1, 2],
# [3], [3, 1], [1, 3], [3, 2], [2, 3], [3, 2, 1], [2, 3, 1], [2, 1, 3], [3, 1, 2], [1, 3, 2], [1, 2, 3]]원소를 하나씩 추가해가며 순열을 구하는 방식. 재귀를 이용하지 않을 수도 있었지만 그냥 재귀를 이용하였다.
중복 순열
def permutations(arr, r):
n = len(arr)
output = []
results = []
def _perm(arr, output, depth, n, r):
if (depth == r):
results.append(output[:])
return
for i in range(n):
new_output = output + [arr[i]]
_perm(arr, new_output, depth + 1, n, r)
_perm(arr, output, 0, n, r)
return results
print(permutations([1, 2, 3], 2))순열 계산시에 썼던 코드를 재사용하여 만들었다.
반응형
'📝 알고리즘 > 수학' 카테고리의 다른 글
| 🧮 부분 집합, 멱집합 구하기 알고리즘 직접 구현! (2) | 2023.01.10 |
|---|---|
| 🧮 조합 알고리즘 직접 구현! (2) | 2023.01.10 |
| ⚡ 고속 거듭제곱 알고리즘 간단설명! (0) | 2022.10.06 |
| [알고리즘, 원리] 유클리드 호제법 (0) | 2022.09.10 |




댓글