반응형

조합과 중복조합 알고리즘을 파이썬으로 구현하기
조합이란?
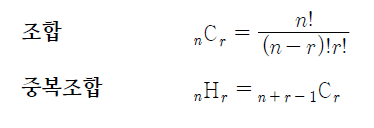
- 원소를 순서없이 나열하는 것
- n개의 원소에서 r개를 조합하면 가짓수는 n!/(n-r)!r!
- 중복조합은 n+r-1개의 원소에서 r개를 조합하는 것과 같다.
- n개의 원소에서 모든 조합 가지수는 2^n - 1
여러가지 조합 알고리즘 구현해보기
기본 조합
n개의 원소가 있는 배열에서 r개를 뽑는다.
조합 점화식에 기반한 방식
def combination(arr, r):
if r == 0:
return [set()]
elif arr == []:
return []
new_arr = arr[:]
item = new_arr.pop()
not_item_comb = combination(new_arr, r)
item_comb = [s|{item} for s in combination(new_arr, r-1)]
return not_item_comb + item_comb
print(combination([1,2,3], 2))- 과정 : nCr = n-1Cr + n-1Cr-1
n-1Cr은 임의의 한 원소를 뽑지 않을 경우, n-1Cr-1은 임의의 그 원소를 뽑았을 경우이다.
그래서 원소 하나를 뽑아 뽑았을 경우에는 추가해준 후 뽑지 않았을 때와 더해준다.
혹은 위의 점화식을 변형시켜 다음과 같이 이용할 수도 있다.
def combination(arr, r):
result = []
if r == 0:
return [set()]
for i in range(len(arr)):
item = arr[i]
for rest in combination(arr[i + 1:], r - 1):
result.append(rest | {item})
return result
print(combination([1, 2, 3, 4], 2))- 과정 : nCr = n-1Cr-1 + n-2Cr-1 + ... + r-1Cr-1
원소들을 하나씩 뺀 상태에서 각 원소를 추가하는 방식으로 한다.
index 체크를 이용한 방식
def combination(arr, r):
n = len(arr)
results = []
def _comb(output, depth, idx):
if (depth == r):
results.append(output.copy())
return
for i in range(idx, n-r+depth+1):
_comb(output|{arr[i]}, depth+1, i+1)
_comb(set(), 0, 0)
return results
print(combination([1, 2, 3, 4], 2))- 과정 : 조합에서는 한번 뽑은 인덱스 이전 인덱스의 원소들은 생각할 필요가 없다. 따라서 DFS 방식으로 각 경우를 체크해준다.
완전탐색 조합
모든 조합 가짓수를 따져준다. 부분집합을 따지는 경우와 같으므로 따로 글을 적었다.
🧮 부분 집합, 멱집합 구하기 알고리즘 직접 구현!
부분집합, 멱집합을 구하는 알고리즘을 파이썬으로 구현해보자. 부분 집합, 멱 집합이란? 부분 집합은 어떤 집합에서 몇몇 원소들만 뽑아서 만든 집합. 부분 집합은 원래 집합에 포함되는 관계
programming4myself.tistory.com
중복 조합
def combination(arr, r):
n = len(arr)
results = []
def _comb(output, depth, idx):
if (depth == r):
results.append(output.copy())
return
for i in range(idx, n): #끝을 n으로 바꿈
_comb(output+[arr[i]], depth+1, i) #i+1를 i로 바꿈
_comb([], 0, 0)
return results
print(combination([1, 2, 3, 4], 2))조합때 썼던 알고리즘에서 값을 중복되게 바꾸어줌. 위의 예시는 index 체크를 이용한 방식을 수정한 것임.
반응형
'📝 알고리즘 > 수학' 카테고리의 다른 글
| 🧮 부분 집합, 멱집합 구하기 알고리즘 직접 구현! (2) | 2023.01.10 |
|---|---|
| 🧮 순열 알고리즘 직접 구현! (0) | 2023.01.10 |
| ⚡ 고속 거듭제곱 알고리즘 간단설명! (0) | 2022.10.06 |
| [알고리즘, 원리] 유클리드 호제법 (0) | 2022.09.10 |




댓글